迪士尼彩乐园负责人 流形中的分块是怎么粘合在一齐的

先看拓扑流形的界说：

6.奥斯梅恩（加拉塔萨雷）：7500万欧元

斯塔姆曾在曼联效力了三个赛季，他坚称自己想要帮助曼联重回辉煌。阿莫林到来之后，曼联的表现并没有明显的改观，这表明曼联还有很多工作要做，斯塔姆表示自己愿意伸出援手。

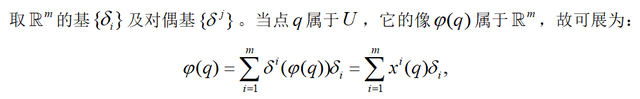
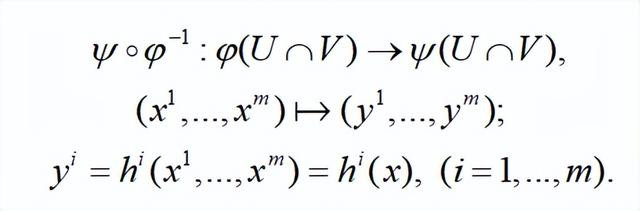
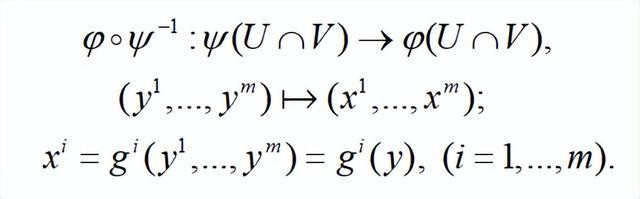
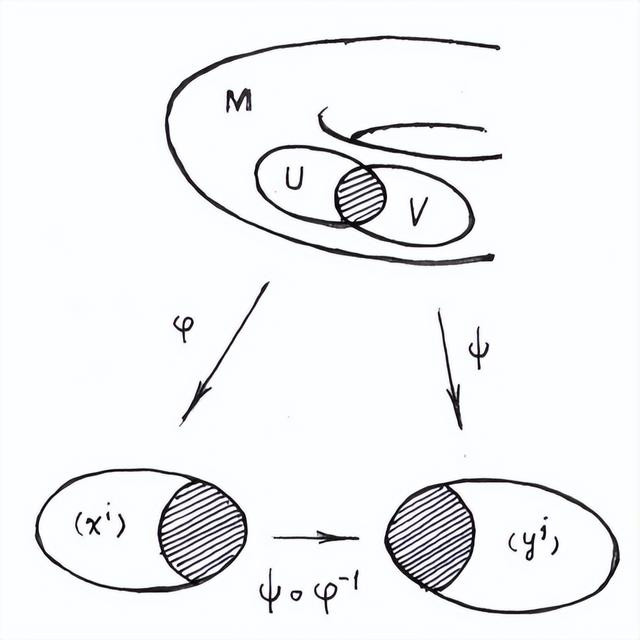
迭置映射（坐标变换）

以上界说的事理无意即是，流形上的每个小块齐对应欧氏空间的一个开区间，而欧氏空间是有坐标系的，是以流形上的每个小块齐有我方的坐标系，称为坐标卡。

流形上两个小块的相交部分不错映射到欧氏空间的某一块内部，从而使得流形上相交的这两个小块不错粘合起来，也即是所谓的迭置映射。（比如A和B的相交部分不错映射到B块所对应的欧氏空间，则A块剩余的部分也不错）

界说：设 M 和 N 是两个微分流形，ϕα 和ψα 分歧是 M 和 N 上的坐标卡。要是ϕα 和ψα 的界说域有杂乱，那么复合映射

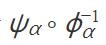
是一个光滑映射，即 C∞ 映射。

应用场景：在微分流形中，迭置映射常用于形色流形在不同坐标卡下的调遣关系。举例，假定 M 是一个微分流形，{Oα} 是 M 的一个开笼罩，关于每个开集 Oα，迪士尼彩乐园存在一个同胚映射ϕα:Oα→Vα，其中 Vα 是Rn 的一个开子集。要是两个开集Oα 和 Oβ 有杂乱，那么复合映射

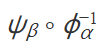
是一个光滑映射，这保证了流形在局部看起来像Rn。

迭置映射响应欧氏空间的小块粘合为流形的局部方式，是局部到合座过渡的基本款式。

迭置映射（或称为坐标变换、映射等）不错将微分流形局部的性质实行到全局，是因为微分流形自己具有局部欧氏空间的性质，且流形的合座结构不错通过局部性质的兼容拼接来形色。

流形是局部具有欧氏空间性质的拓扑空间，即流形上每少量的近邻和欧氏空间的一个开集是同胚的。这种局部欧氏空间的性质使得咱们不错在流形的每一个局部界说坐标系和微分结构，从而商讨流形的局部性质。

预计词，微分流形的魔力不仅在于其局部性质，更在于其合座结构。流形的合座结构是通过将局部性质以兼容的方式拼接起来而获取的。这种拼接经由需要依赖于迭置映射，也即是坐标变换。通过迭置映射，咱们不错确保流形上不同局部区域的坐标系和微分结构能够平滑地过渡，从而酿成一个调处的合座结构。

因此，当咱们商讨微分流形的全局性质时，不错诈欺迭置映射将局部性质实行到全局。具体来说，咱们不错先在流形的每一个局部区域商讨其性质，然后通过迭置映射将这些局部性质拼接起来，获取流形的全局性质。这种步伐使得咱们能够愈加潜入地雄厚微分流形的结构和动作。

迪士尼彩乐园负责人

• 迪士尼彩乐园负责人
• 种的
• 怎么
• 流行
• 分块